Ukuran Pemusatan Data
| Rumus | Data Tunggal | Data Berkelompok |
| Rataan (mean) | ||
| Modus | Mo = nilai dg frekuensi tertinggi/paling sering muncul | |
| Median | ganjil genap | |
| Kuartil | ||
| Desil |
Untuk data tunggal, data diurutkan terlebih dahulu sehingga saat mencari median, kuartil dan desil kita tidak salah menentukan  -nya.
-nya.
Yang pasti, hafal rumusnya juga harus tau simbol dan cara menentukan nilainya yah…lihat keterangan berikut ini : Ket :
| = nilai ke- i (data tunggal) | |
| = nilai tengah kelas ke-i (data berkelompok) | |
| = frekuensi ke- i | |
| = jumlah frekuensi/banyaknya data | |
| = tepi bawah = (BB – 0,5) | |
| = frekuensi kelas modus – frek kls di atasny | |
| = frekuensi kelas modus – frek kls di bawahny | |
| = interval/panjang kelas=BA-BB+1 | |
| = frekuensi kumulatif sebelum kelas yg dimaksud | |
| = frekuensi kelas Median | |
| = frekuensi kelas kuartil | |
| = frekuensi kelas desil | |
| *letak kls Median | = |
| *letak kls Kuartil | = |
| *letak kls Desil | = |
langsung ke contoh dan pembahasan soal data tunggal yuk…
1. diketahui data sebagai berikut : 5, 6, 4, 8, 7, 3, 8, 9, 4, 10 . Tentukan 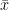 , Modus, Median, Kuartil ke-3, dan desil ke-7 !
, Modus, Median, Kuartil ke-3, dan desil ke-7 !
jawab :
urutan data:
| 3, | 4, | 4, | 5, | 6, | 7, | 8, | 8, | 9, | 10 |
0 komentar:
Posting Komentar